Сопротивление в электрических цепях бывает двух видов – активное и реактивное. Активное представлено резисторами, лампами накаливания, нагревательными спиралями и пр. Другими словами, всеми элементами, в которых протекающий ток непосредственно совершает полезную работу или, частный случай, вызывает желаемый нагрев проводника. В свою очередь, реактивное – это обобщающий термин. Под ним понимают емкостное и индуктивное сопротивление. В элементах цепи, обладающих реактивным сопротивлением, при прохождении электрического тока происходят различные промежуточные преобразования энергии. Конденсатор (емкость) накапливает заряд, а затем отдает его в контур. Другой пример – индуктивное сопротивление катушки, в которой часть электрической энергии превращается в магнитное поле.
На самом деле «чистых» активных или реактивных сопротивлений нет. Всегда присутствует противоположная составляющая. Например, при расчете проводов для линий электропередач большой протяженности, учитывают не только активное сопротивление, но и емкостное. А рассматривая индуктивное сопротивление, нужно помнить, что как проводники, так и источник питания вносят свои корректировки в расчеты.
Определяя общее сопротивление участка цепи, необходимо сложить активную и реактивную составляющие. Причем, получить прямую сумму обычным математическим действием невозможно, поэтому используют геометрический (векторный) способ сложения. Выполняют построение прямоугольного треугольника, два катета которого представляют собой активное и индуктивное сопротивление, а гипотенуза – полное. Длина отрезков соответствует действующим значениям.
Рассмотрим индуктивное сопротивление в цепи переменного тока. Представим простейшую цепь, состоящую из источника питания (ЭДС, E), резистора (активная составляющая, R) и катушки (индуктивность, L). Так как индуктивное сопротивление возникает благодаря ЭДС самоиндукции (E си) в витках катушки, то очевидно, что оно возрастает с увеличением индуктивности цепи и ростом значения протекающего по контуру тока.
Закон ома для такой цепи выглядит как:
Определив производную тока от времени (I пр), можно вычислить самоиндукцию:
Знак «-» в уравнении указывает на то, что действие E си направлено против изменения значения тока. Правило Ленца гласит, что при любом изменении тока возникает ЭДС самоиндукции. А так как такие изменения в цепях переменного тока естественны (и постоянно происходят), то E си формирует существенное противодействие или, что также верно, сопротивление. В случае источника питания постоянного тока данная зависимость не выполняется и при попытке подключить катушку (индуктивность) в подобную цепь произошло бы классическое к.з.
Для преодоления E си источник питания должен создавать на выводах катушки такую разность потенциалов, чтобы ее хватило, как минимум, на компенсацию сопротивления E си. Отсюда следует:
Другими словами, напряжение на индуктивности численно равно электродвижущей силе самоиндукции.
Так как с ростом тока в цепи увеличивается магнитное поле, в свою очередь генерирующее вихревое поле, вызывающее рост противотока в индуктивности, то можно сказать, что имеет место смещение фаз между напряжением и током. Отсюда следует одна особенность: так как ЭДС самоиндукции препятствует любому изменению тока, то при его возрастании (первая четверть периода на синусоиде) происходит генерация полем противотока, а вот при падении (вторая четверть) наоборот – индуцированный ток сонаправлен с основным. То есть, если теоретически допустить существование идеального источника питания без внутреннего сопротивления и индуктивность без активной составляющей, то колебания энергии «источник – катушка» могли бы происходить неограниченное время.
Сопротивление в электрических цепях бывает двух видов – активное и реактивное. Активное представлено резисторами, лампами накаливания, нагревательными спиралями и пр. Другими словами, всеми элементами, в которых протекающий ток непосредственно совершает полезную работу или, частный случай, вызывает желаемый нагрев проводника. В свою очередь, реактивное – это обобщающий термин. Под ним понимают емкостное и индуктивное сопротивление. В элементах цепи, обладающих реактивным сопротивлением, при прохождении электрического тока происходят различные промежуточные преобразования энергии. Конденсатор (емкость) накапливает заряд, а затем отдает его в контур. Другой пример – индуктивное сопротивление катушки, в которой часть электрической энергии превращается в магнитное поле.
На самом деле «чистых» активных или реактивных сопротивлений нет. Всегда присутствует противоположная составляющая. Например, при расчете проводов для линий электропередач большой протяженности, учитывают не только активное сопротивление, но и емкостное. А рассматривая индуктивное сопротивление, нужно помнить, что как проводники, так и источник питания вносят свои корректировки в расчеты.
Определяя общее сопротивление участка цепи, необходимо сложить активную и реактивную составляющие. Причем, получить прямую сумму обычным математическим действием невозможно, поэтому используют геометрический (векторный) способ сложения. Выполняют построение прямоугольного треугольника, два катета которого представляют собой активное и индуктивное сопротивление, а гипотенуза – полное. Длина отрезков соответствует действующим значениям.
Рассмотрим индуктивное сопротивление в цепи переменного тока. Представим простейшую цепь, состоящую из источника питания (ЭДС, E), резистора (активная составляющая, R) и катушки (индуктивность, L). Так как индуктивное сопротивление возникает благодаря ЭДС самоиндукции (E си) в витках катушки, то очевидно, что оно возрастает с увеличением индуктивности цепи и ростом значения протекающего по контуру тока.
Закон ома для такой цепи выглядит как:
Определив производную тока от времени (I пр), можно вычислить самоиндукцию:
Знак «-» в уравнении указывает на то, что действие E си направлено против изменения значения тока. Правило Ленца гласит, что при любом изменении тока возникает ЭДС самоиндукции. А так как такие изменения в цепях переменного тока естественны (и постоянно происходят), то E си формирует существенное противодействие или, что также верно, сопротивление. В случае источника питания постоянного тока данная зависимость не выполняется и при попытке подключить катушку (индуктивность) в подобную цепь произошло бы классическое к.з.
Для преодоления E си источник питания должен создавать на выводах катушки такую разность потенциалов, чтобы ее хватило, как минимум, на компенсацию сопротивления E си. Отсюда следует:
Другими словами, напряжение на индуктивности численно равно электродвижущей силе самоиндукции.
Так как с ростом тока в цепи увеличивается магнитное поле, в свою очередь генерирующее вихревое поле, вызывающее рост противотока в индуктивности, то можно сказать, что имеет место смещение фаз между напряжением и током. Отсюда следует одна особенность: так как ЭДС самоиндукции препятствует любому изменению тока, то при его возрастании (первая четверть периода на синусоиде) происходит генерация полем противотока, а вот при падении (вторая четверть) наоборот – индуцированный ток сонаправлен с основным. То есть, если теоретически допустить существование идеального источника питания без внутреннего сопротивления и индуктивность без активной составляющей, то колебания энергии «источник – катушка» могли бы происходить неограниченное время.
При включении катушки индуктивности в цепь переменного тока, под действием непрерывно изменяющегося напряжения происходят изменения этого тока. В свою очередь, эти изменения вызывают генерацию магнитного поля, которое периодический возрастает или убывает. Под его влиянием в катушке индуцируется встречное напряжение, препятствующее изменениям тока. Таким образом, протекание тока происходит под непрерывным противодействием, получившим название индуктивного сопротивления.
Данная величина связана напрямую с частотой приложенного напряжения (f) и значением индуктивности (L). Формула индуктивного сопротивления будет выглядеть следующим образом: XL = 2πfL. Прямая пропорциональная зависимость, в случае необходимости, позволяет путем преобразования основной формулы вычислить частоту или значение индуктивности.
Содержание
От чего зависит индуктивное сопротивление
Под действием переменного тока, проходящего по проводнику, вокруг этого проводника образуется переменное магнитное поле. Действие этого поля приводит к наведению в проводнике электродвижущей силы обратного направления, известной еще как ЭДС самоиндукции. Противодействие или сопротивление ЭДС переменному току получило название реактивного индуктивного сопротивления.

Данная величина зависит от многих факторов. В первую очередь на нее оказывает влияние как значение тока не только в собственном проводнике, но и в соседних проводах. То есть увеличение сопротивления и потока рассеяния происходит по мере увеличения расстояния между фазными проводами. Одновременно снижается воздействие соседних проводов.
Существует такое понятие, как погонное индуктивное сопротивление, которое вычисляется по формуле: X0 = ω x (4,61g x (Dср/Rпр) + 0,5μ) x 10-4 = X0’ + X0’’, в которой ω является угловой частотой, μ – магнитной проницаемостью, Dср – среднегеометрическим расстоянием между фазами ЛЭП, а Rпр – радиусом провода.
Величины X0’ и X0’’ представляют собой две составные части погонного индуктивного сопротивления. Первая из них X0’ представляет собой внешнее индуктивное сопротивление, зависящее только от внешнего магнитного поля и размеров ЛЭП. Другая величина – X0’’ является внутренним сопротивлением, зависящим от внутреннего магнитного поля и магнитной проницаемости μ.
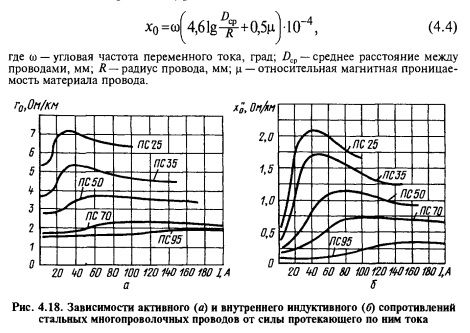
На линиях электропередачи высокого напряжения от 330 кВ и более, проходящие фазы расщепляются на несколько отдельных проводов. Например, при напряжении 330 кВ фаза разделяется на два провода, что позволяет снизить индуктивное сопротивление примерно на 19%. Три провода используются при напряжении 500 кВ – индуктивное сопротивление удается снизить на 28%. Напряжение 750 кВ допускает разделение фаз на 4-6 проводников, что способствует снижению сопротивления примерно на 33%.
Погонное индуктивное сопротивление имеет величину в зависимости от радиуса провода и совершенно не зависит от сечения. Если радиус проводника будет увеличиваться, то значение погонного индуктивного сопротивления будет соответственно уменьшаться. Существенное влияние оказывают проводники, расположенные рядом.
Индуктивное сопротивление в цепи переменного тока
Одной из основных характеристик электрических цепей является сопротивление, которое может быть активным и реактивным. Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу.
К реактивному относятся индуктивное и емкостное сопротивления, находящиеся в промежуточных преобразователях электроэнергии – индуктивных катушках и конденсаторах. Эти параметры в обязательном порядке учитываются при выполнении различных расчетов. Например, для определения общего сопротивления участка цепи, складываются активная и реактивная составляющие. Сложение осуществляется геометрическим, то есть, векторным способом, путем построения прямоугольного треугольника. В нем оба катета являются обоими сопротивлениями, а гипотенуза – полным. Длина каждого катета соответствует действующему значению того или иного сопротивления.
В качестве примера можно рассмотреть характер индуктивного сопротивления в простейшей цепи переменного тока. В нее входит источник питания, обладающий ЭДС (Е), резистор, как активная составляющая (R) и катушка, обладающая индуктивностью (L). Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру.
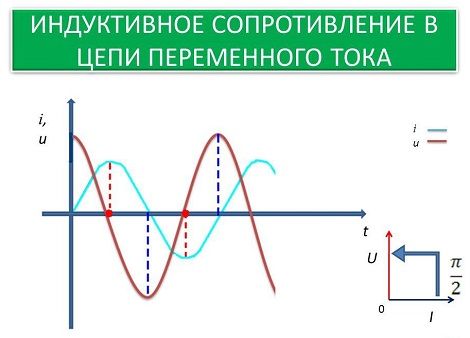
Таким образом, закон Ома для такой цепи переменного тока будет выглядеть в виде формулы: Е + Еси = I x R. Далее с помощью этой же формулы можно определить значение самоиндукции: Еси = -L x Iпр, где Iпр является производной тока от времени. Знак «минус» означает противоположное направление Еси по отношению к изменяющемуся значению тока. Поскольку в цепи переменного тока подобные изменения происходят постоянно, наблюдается существенное противодействие или сопротивление со стороны Еси. При постоянном токе данная зависимость отсутствует и все попытки подключения катушки в такую цепь привели бы к обычному короткому замыканию.
Для преодоления ЭДС самоиндукции, на выводах катушки источником питания должна создаваться такая разность потенциалов, чтобы она могла хотя-бы минимально компенсировать сопротивление Еси (Uкат = -Еси). Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности. В результате, между током и напряжением происходит смещение фаз.
Индуктивное сопротивление катушки
Катушка индуктивности относится к категории пассивных компонентов, используемых в электронных схемах. Она способна сохранять электроэнергию, превращая ее в магнитное поле. В этом и состоит ее основная функция. Катушка индуктивности по своим характеристиками и свойствам напоминает конденсатор, сохраняющий энергию в виде электрического поля.
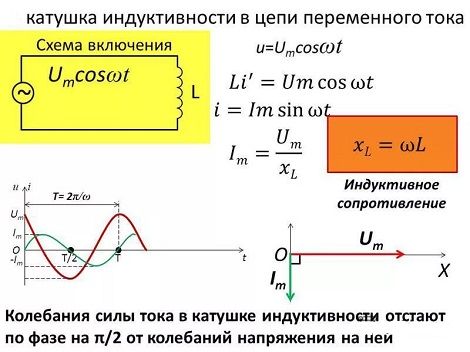
Индуктивность, измеряемая в Генри, заключается в появлении вокруг проводника с током магнитного поля. В свою очередь, связано с электродвижущей силой, которая противодействует приложенному переменному напряжению и силе тока в катушке. Данное свойство и есть индуктивное сопротивление, находящееся в противофазе с емкостным сопротивлением конденсатора. Индуктивность катушки возможно повысить за счет увеличения количества витков.
Для того чтобы выяснить, чему равно индуктивное сопротивление катушки, следует помнить, что оно, в первую очередь, противодействует переменному току. Как показывает практика, каждая индуктивная катушка сама по себе имеет определенное сопротивление.
Прохождение переменного синусоидального тока через катушку, приводит к возникновению переменного синусоидального напряжения или ЭДС. В результате, возникает индуктивное сопротивление, определяемое формулой: XL = ωL = 2πFL, в которой ω является угловой частотой, F – частотой в герцах, L – индуктивностью в генри.



