Реактивная мощность обусловлена способностью реактивных элементов накапливать и отдавать электрическую или магнитную энергию.
Eмкостная нагрузка в цепи переменного тока за время половины периода накапливает заряд в обкладках конденсаторов и отдаёт его обратно в источник.
Индуктивная нагрузка накапливает магнитную энергию в катушках и возвращает её в источник питания в виде электрической энергии.
Напряжение на выводах реактивного элемента будет достигать максимального значения во время смены направления тока, следовательно, расхождение во времени между напряжением и током в пределах элемента составит четверть периода (сдвиг фаз 90°).
Угол сдвига фаз φ в цепи нагрузки определяется соотношением активного и реактивного сопротивлений нагрузки.
Реактивная мощность характеризует потери, созданные реактивными элементами в цепи переменного тока, и выражается формулой Q = UIsinφ.
Природу потерь в цепи с реактивными элементами можно рассмотреть с помощью графиков на рисунках.
При отсутствии активной составляющей в нагрузке, сдвиг фаз между напряжением и током составит 90°.
В начале периода, когда напряжение максимально – ток будет равен нулю, следовательно, мгновенное значение мощности UI в это время будет равно нулю.
В течении первой четверти периода, мощность можно видеть на графике, как произведение UI, которое станет равным нулю при максимуме тока и нулевом значении напряжения.
В следующую четверть периода на графике UI принимает отрицательное значение, следовательно, мощность возвращается обратно в источник питания. То же самое произойдёт и в отрицательном полупериоде тока. В результате средняя (активная) потребляемая мощность P avg за период будет равна нулю.
В таком случае:
Реактивная мощность Q = UIsin90° = UI
Потребляемая мощность P = UIcos90° = 0
Полная мощность S = UI = √(P² + Q²) будет равна реактивной мощности
Коэффициент мощности P/S = 0
При отсутствии реактивных элементов и сдвига фаз в нагрузках, мгновенная мощность в полупериоде Umax*Imax будет максимальной, и в следующем полупериоде произведение отрицательного напряжения с отрицательным током дадут положительный результат – полезную мощность в нагрузке.
В этом случае:
Реактивная мощность Q = UIsin0 = 0
Потребляемая мощность P = UIcos0 = UI
Полная мощность S = UI = √(P² + Q²) будет равна потребляемой мощности
Коэффициент мощности P/S = 1
Ниже представлен рисунок графиков со сдвигом фаз 45°, для случая равенства активного и реактивного сопротивлений в нагрузке.
Здесь:
Реактивная мощность Q = UIsin45° = 0.71UI
Потребляемая мощность P = UIcos45° = 0.71UI
Полная мощность S = √(P² + Q²) = UI
Коэффициент мощности P/S = 0.71
В примерах рассмотрены случаи с индуктивной нагрузкой, когда ток отстаёт от напряжения (положительный сдвиг фаз).
В случаях с ёмкостной нагрузкой, процессы и расчёты аналогичны, только напряжение будет отставать от тока (отрицательный сдвиг фаз).
Угол сдвига фаз в сети определится соотношением активного и реактивного сопротивлений нагрузок в параллельном соединении следующим образом:
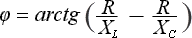
XL и XС соответственно индуктивное и ёмкостное сопротивление нагрузок.
Преобладание индуктивных нагрузок будет уменьшать общее индуктивное сопротивление.
Из выражения видно, что угол в этом случае будет принимать положительный знак, а преобладание ёмкостных нагрузок будет уменьшать ёмкостное сопротивление и вызывать отрицательный сдвиг. При равенстве индуктивного и ёмкостного сопротивлений, угол сдвига будет равен нулю.
В бытовых и производственных потребителях индуктивное сопротивление обычно существенно преобладает над ёмкостным.
Подробнее о вычислениях общего угла сдвига φ для вариантов соединений активного и реактивного сопротивлений в нагрузках можно ознакомиться на страничке электрический импеданс.
Содержание
Компенсация реактивной мощности
Огромное количество индуктивных нагрузок в сети суммарно обладает колоссальной реактивной мощностью, которая возвращается в генераторы и не совершает никакой полезной работы, расходуя энергию на нагрев кабелей и проводов ЛЭП, перегружает трансформаторы, снижая их КПД, тем самым уменьшая пропускную способность активных токов.
Если параллельно индуктивной нагрузке подключить конденсатор, фаза тока в цепи источника будет смещаться в противоположную сторону, компенсируя угол, созданный индуктивностью нагрузки. При определённом соотношении номиналов, можно добиться отсутствия сдвига фаз, следовательно, и отсутствия реактивных токов в цепи источника питания.
Ёмкость конденсатора определяется реактивным (индуктивным) сопротивлением нагрузки, которое необходимо компенсировать:
C = 1/(2πƒX),
X = U²/Q – реактивное сопротивление нагрузки,
Q – реактивная мощность нагрузки.
Компенсация реактивных токов в сети позволяет значительно уменьшить потери на активном сопротивлении проводов ЛЭП, кабелей и обмоток трансформаторов питающей сети.
В целях компенсации реактивной мощности на производственных предприятиях, где основными потребителями энергии являются асинхронные электродвигатели, индукционные печи, люминесцентное освещение, которые обладают индуктивным сопротивлением, часто применяют специальные конденсаторные установки, способные в ручном или автоматическом режиме поддерживать нулевой сдвиг фаз, тем самым минимизировать реактивные потери.
В масштабах энергосистемы компенсация происходит непосредственно на электростанциях путём контроля сдвига фаз и обеспечения соответствующего тока подмагничивания роторных обмоток синхронных генераторов станций.
Компенсация реактивной мощности – одна из составляющих комплекса мер по Коррекции Коэффициента Мощности (ККМ) в электросети (Power Factor Correction – PFC в англоязычной литературе). Применяется в целях уменьшения потерь электроэнергии, как на паразитную реактивную, так и нелинейную составляющую искажений тока в энергосистеме. Более подробно с материалом о ККМ (PFC) можно ознакомиться на странице – коэффициент мощности.
Онлайн-калькулятор расчёта реактивной мощности и её компенсации.
Достаточно вписать значения и кликнуть мышкой в таблице.
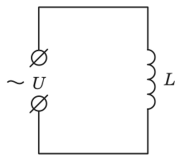
Индуктивная нагрузка в цепи переменного тока
Подключим к сети переменного напряжения U = Umsincot катушку индуктивности L с малым активным сопротивлением R = О (рис. 14.6). Когда по катушке идет переменный ток, в ней возникает ЭДС самоиндукции, которая по закону Ленца противодействует приложенному напряжению:
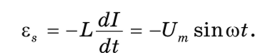
Решение этого дифференциального уравнения относительно тока имеет вид:
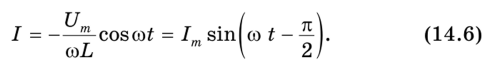
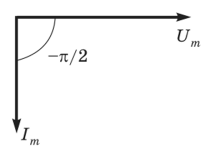
Рис. 14.7. Векторная диаграмма при индуктивной нагрузке
Видно, что в цепи с индуктивной нагрузкой ток отстает по фазе от напряжения на 90° (рис. 14.7), поэтому средняя мощность, выделяющаяся на чисто индуктивной нагрузке, равна нулю:
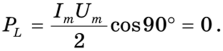
Сопротивление индуктивности переменному току на основании закона Ома
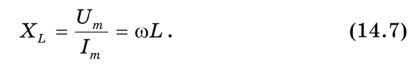
Видно, что постоянному току (со = 0) чистая индуктивность L не оказывает сопротивления (Хь = 0), а ее сопротивление переменному току растет пропорционально частоте.
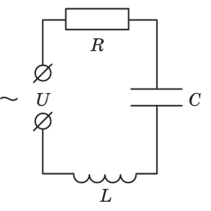
Рис. 14.8. Омическая, емкостная и индуктивная нагрузки в цепи переменного тока
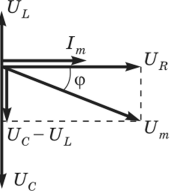
Рис. 14.9. Векторная диаграмма для последовательной цепи переменного тока
Рассмотрим цепь переменного тока, содержащую последовательно соединенные нагрузки трех видов (рис. 14.8). Для цепи постоянного тока ее полное сопротивление определялось бы как сумма сопротивлений всех последовательно включенных составляющих.
В последовательной цепи переменного тока общим для всех нагрузок цепи является ток, а напряжения на каждом из элементов цепи сдвинуты по фазе относительно тока: напряжение на активной нагрузке совпадает по фазе с током, напряжение на емкости отстает от тока на 90°, а напряжение на индуктивности опережает ток по фазе на 90°.
Поэтому при определении полного сопротивления электрической цепи, представленной на рис. 14.8, необходимо учитывать фазовые соотношения между током и напряжением, зависящие от вида нагрузки.
Рассчитать ток в такой цепи можно с помощью векторной диаграммы, представленной на рис. 14.9. Из нее видно, что
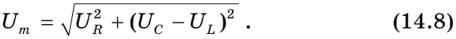
Поскольку амплитуды напряжений связаны с амплитудой тока соотношениями UR-ImR, Uc– ImXc, UL-ImXL, то после подстановки получим
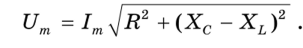
Теперь можем определить полное сопротивление Z (импеданс) последовательной цепи переменному току, учитывая формулы (14.5) и (14.7):
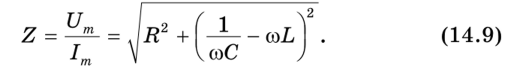
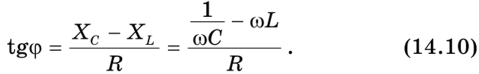
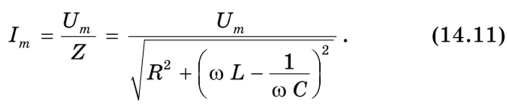
Видно, что импеданс Z рассматриваемой цепи зависит не только от параметров нагрузок R, С и L, но и от частоты со переменного напряжения. На рис. 14.10 приведены графики зависимости сопротивлений разных нагрузок от частоты переменного тока.
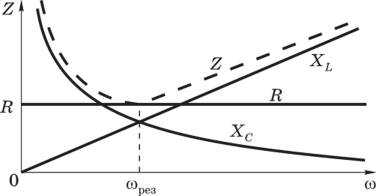
Рис. 14.10. Зависимость активного. индуктивногоXL, емкостногоХс и полного Z (пунктир) сопротивлений цепи от частоты тока
Импеданс принимает наименьшее значение, равное активной нагрузке R, при со L =-. В этом случае сила тока
в цепи максимальна и в цепи наступает явление электрического резонанса. Поэтому частота сорез – Д— , на которой
наблюдается это явление, называется резонансной частотой данной цепи. При этом Z = R, а сдвиг фаз между током и напряжением ф = 0, т.е. на этой частоте цепь ведет себя как чисто активная нагрузка R.
В цепях переменного тока нагрузка, которая потребляет электрическую мощность, называется активным сопротивлением, нагрузка, которая не потребляет электрической мощности – называется реактивным сопротивлением.
Активное сопротивление – проводники, растворы, газы и т.д.
Реактивное сопротивление – катушки индуктивности и конденсаторы.
Активное сопротивление.При включении в цепь переменного тока активного сопротивления проходящий по этому сопротивлению ток изменяется по такому же закону, как и напряжение, создаваемое источником переменного тока. Следовательно, Iи U изменяются по волнообразной кривой – синусоиде, причем они будут иметь одинаковый период, одновременно достигать максимума и проходят через ноль, то принято называть такой характер изменения – совпадением по фазе.
При включении в цепь переменного тока активного сопротивления, Iи U совпадают по фазе.Закон ОмаI =

Индуктивное сопротивление.При включении катушки в цепь переменного тока в ней возникает ЭДС самоиндукции, которая по закону Ленца стремится препятствовать изменению вызывающего её тока. Это означает, что катушка индуктивности оказывает сопротивление прохождению переменного тока, которое называется индуктивным сопротивлением XL
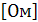
и зависит от L катушки и частоты тока.
XL =
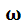
L = 2
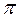
fL,
где L– индуктивность
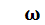
– угловая частота = 2
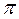
f
F – частота в Гц
Закон Ома. I =
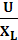
=
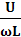
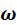
= 2
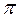
f
При включении в цепь переменного тока индуктивного сопротивления ток отстает по фазе от напряжения на четверть периода или напряжение опережает ток по фазе на четверть периода (
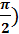
.

За период индуктивное сопротивление не отдает и не потребляет электрической энергии и среднее значении мощности за период равно нулю, т.к. происходит непрерывная циркуляция электрической энергии между источником тока и RL не создающая никакой работы.
Для того чтобы подчеркнуть указанную особенность индуктивного сопротивления, его относят к группе реактивных сопротивлений, т.е. сопротивления, которые в цепи переменного тока не потребляют электрической мощности.
Емкостное сопротивление.Конденсатор оказывает прохождению переменного тока сопротивление, т.к. происходит непрерывный процесс его заряда и разряда: при этом через конденсатор проходит переменный ток, это и называется емкостным сопротивлениемХс
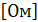
– зависит от величины емкости конденсатора и частоты изменения тока. Чем больше емкость конденсатора, тем меньшее сопротивления оказывает конденсатор прохождению переменного тока, чем больше частота, тем меньше его Хс.

Xc =
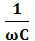
=
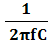
C =
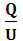
, [Ф] – фарад
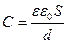
–емкость конденсатора
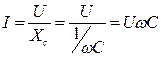
Ток в цепи конденсатора опережает по фазе напряжение на четверть периода (угол 90 градусов) или напряжение отстает по фазе от тока на четверть периода (на угол 90 градусов).
Конденсатор, как и катушка индуктивности в цепи переменного тока не потребляет активной мощности. Средняя мощность, потребляемая конденсатором за период равна нулю.
При последовательном соединении:При параллельном соединении:


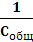
=
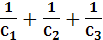
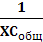
=
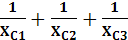
Дата добавления: 2017-11-21 ; просмотров: 2913 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ


