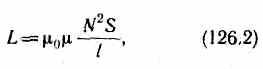Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био — Савара—Лапласа (см. (110.2)), пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току I в контуре:
где коэффициент пропорциональности L называется индуктивностью контура.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Из выражения (126.1) определяется единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:
Рассчитаем индуктивность бесконечно длинного соленоида. Согласно (120.4), полный магнитный поток через соленоид
(потокосцепление) равен 0(N 2 I/l)S. Подставив это выражение в формулу (126.1), получим
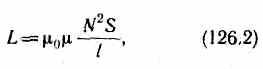
т. е. индуктивность соленоида зависит от числа витков соленоида N, его длины l, площади S и магнитной проницаемости вещества, из которого изготовлен сердечник соленоида.
Можно показать, что индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится. В этом смысле индуктивность контура — аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды (см. §93).
Применяя к явлению самоиндукции закон Фарадея (см. (123.2)), получим, что э.д.с. самоиндукции
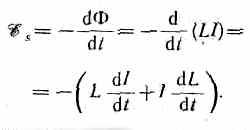
Если контур не деформируется и магнитная проницаемость среды не изменяется (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L=const и
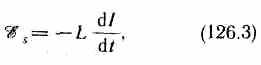
где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем.
Если ток со временем возрастает, то
dI/dt>0 и ξs 0, т. е. индукционный
ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, обладая определенной индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность контура.
Содержание
§ 127. Токи при размыкании и замыкании цепи
При всяком изменении силы тока в проводящем контуре возникает э.д.с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.
Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. ξ, резистор сопротивлением R и катушку индуктивностью L. Под действием внешней э.д.с. в цепи течет постоянный ток
(внутренним сопротивлением источника тока пренебрегаем).
В момент времени t=0 отключим источник тока. Ток через катушку индуктивности L начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции ξs=-LdI/dt, препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется законом Ома I=ξs/R, или
Разделив в выражении (127.1) переменные, получим dI/I=–(R/L)dt. Интегрируя
это уравнение по I (от I до I) и t (от 0 до t), находим ln(I/I)=-Rt/L, или

где =L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что т есть время, в течение которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника э.д.с. сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше т и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При замыкании цепи помимо внешней э.д.с.ξ возникает э.д.с. самоиндукции
правилу Ленца, возрастанию тока. По закону Ома, IR=ξ+ξs, или
Введя новую переменную u=IR-ξ, преобразуем это уравнение к виду du/u=-dt/,
где 1 — время релаксации.
В момент замыкания (t=0) сила тока I=0 и u=-ξ. Следовательно, интегрируя по и (от -ξ до IR — ξ) и t (от 0 до t).
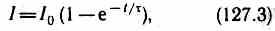
где I=ξ/R — установившийся ток (при t)
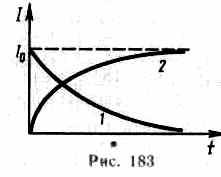
Таким образом, в процессе включения источника э.д.с. нарастание силы тока в цепи задается функцией (127.3) и определяется кривой 2 на рис. 183. Сила тока возрастает от начального значения I=0 и асимптотически стремится к установившемуся значению I=ξ/R. Скорость нарастания тока определяется тем же временем релаксации =L/R, что и убывание тока. Установление тока происходит тем быстрее, чем меньше индуктивность цепи и больше ее сопротивление.
Оценим значение э.д.с. самоиндукции ξs, возникающей при мгновенном увеличении сопротивления цепи постоянного тока от R До R. Предположим, что мы размыкаем контур, когда в нем течет установившийся ток I=ξ/R. При размыкании цепи ток изменяется по формуле (127.2). Подставив в нее выражение для I и , получим
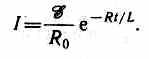
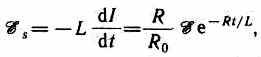
т. е. при значительном увеличении сопротивления цепи (R/R>>1) обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.
Индуктивность контура — это коэффициент пропорциональности между постоянным током, текущим в заданном замкнутом контуре, и потоком вектора магнитной индукции, создаваемым этим током через поверхность, окружённой этим контуром. Обозначение — , размерность — Гн (генри). Формульно:
- где
- Ф — поток вектора магнитной индукции,
- — индуктивность контура,
- — сила тока в контуре.
В большинстве задач данный параметр задан в условии, однако есть одна система, в которой данный параметр является расчётным. Это соленоид (рис. 1). Соленоидом называется провод, согнутый в виде спирали (он же, в принципе, катушка индуктивности). Формульно:
- где
- — индуктивность соленоида,
- — относительная магнитная проницаемость среды (табличные данные),
- м*кг* * ,
- — число витков,
- — площадь поперечного сечения витка,
- — длинна катушки.
Немного о — относительной магнитной проницаемости среды. Чаще всего в школьных задачах соленоид пустотелый, т.е. внутри него (витков) воздух, тогда . Иногда в него помещают сердечник, т.е. болванку формой повторяющую внутреннюю геометрию соленоида, тогда 1" title="displaystyle mu >1" > и по веществу, из которого состоит сердечник, можно в таблицах найти значение магнитной проницаемости.
Для ряда задач существует всё тот же вопрос о параллельном и последовательном соединении индуктивностей. Будем считать, что взаимной индукции нет (т.е. один контур экранирован от второго). Тогда:
- при параллельном подключении:
- где
- — общая индуктивность системы контуров,
- — сумма обратных индуктивностей, входящих в цепь.
В случае двух элементов, соединённых параллельно:
- при последовательном подключении:
- где
- — общая индуктивность системы контуров,
- — сумма индуктивностей, входящих в цепь.
Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био-Савара-Лапласа пропорциональна току. Поэтому сцепленный с контуром магнитный поток пропорционален току в контуре:
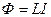
где коэффициент пропорциональности L называется индуктивностью контура.
Пример: индуктивность длинного соленоида.
Потокосцепление соленоида (полный магнитный поток сквозь соленоид):
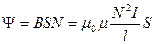
, откуда:
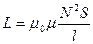
где N — число витков соленоида, l — его длина, S — площадь, μ— магнитная проницаемость сердечника.
Индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится.
В этом смысле индуктивность контура — аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды.
32. Самоиндукция.
При изменении силы тока в контуре будет изменяться и сцепленный с ним магнитный поток, а это, в свою очередь будет индуцировать ЭДС в этом контуре. Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Единица индуктивности — генри (Гн): 1Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в IA равен 1В6 (1Гн=1Вб/А=1В-c/А).
Из закона Фарадея ЭДС самоиндукции
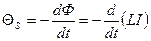
.
Если контур не деформируется и магнитная проницаемость среды не
изменяется, то L = const и ЭДС самоиндукции:
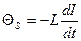
где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем.
Если ток со временем возрастает, то
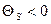
, т.е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его возрастание.
Если ток со временем убывает, то
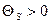
, т.е. ток самоиндукции имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание.
Таким образом, контур, обладая определенной индуктивностью, приобретает электрическую "инертность".
33. Токи при размыкании и замыкании цепи.
При всяком изменении сипы тока в проводящем контуре возникает ЭДС самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции.
Пусть в цепи сопротивлением R и индуктивностью L под действием внешней ЭДС Θтечет постоянный ток
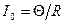
. В момент времени t = 0 выключим источник тока. Возникает ЭДС самоиндукции
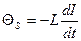
, препятствующая уменьшению тока. Ток в цепи определяется законом Ома
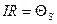
, или
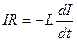
. Разделяем переменные:
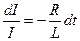
, и интегрируем по I (oт
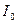
до I) и по t (от 0 до t):
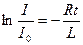
, или
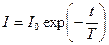
(кривая 1)
где
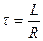
постоянная, называемая временем релаксации — время, в течение которого сила тока уменьшается в ераз.
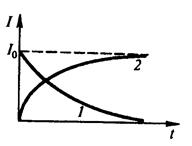
Таким образом, при выключении источника тока сила тока убывает по экспоненциальному закону (а не мгновенно).
Оценим значение ЭДС самоиндукции при мгновенном увеличении сопротивления от
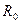
до R:
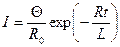
, откуда
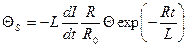
Т.е. при резком размыканииконтура (
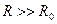
) ЭДС самоиндукции
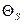
может во много раз превысить Θ, что может привести к пробою изоляции и выводу из строя измерительных приборов.
При замыкании цепи помимо внешней ЭДС Θвозникает ЭДС самоиндукции
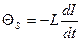
, препятствующая возрастанию тока. По закону Ома,
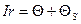
или
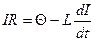
. Можно показать, что решение этого уравненияимеет вид:
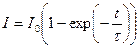
(кривая 2)
где
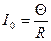
установившийся ток (при
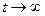
)
Таким образом, при включении источника тока сила тока возрастает по экспоненциальному закону (а не мгновенно).
34. Взаимная индукция.
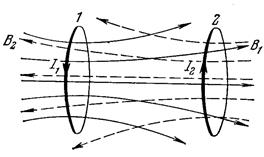
Взаимной индукцией называется явление возбуждения ЭДС электромагнитной индукции в одной электрической цепи при изменении электрического тока в другой цепи или при изменении взаимного расположения этих двух цепей.
Рассмотрим два неподвижных контура 1 и 2 с токами I1 и I2, расположенных достаточно близко друг от друга. При протекании в контуре 1 тока I1 магнитный поток пронизывает второй контур:
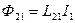
, аналогично
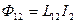
Коэффициенты пропорциональности
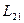
и
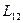
равны друг другу
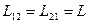
и называются взаимной индуктивностью контуров.
При изменении силы тока в одном из контуров, в другом индуцируется ЭДС:
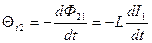
,
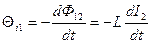
Взаимная индуктивность контуров зависит от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей контуры среды.
и током 1^ создает поле Магнитный поток сквозь один
Для примера рассчитаем взаимную индуктивность двух катушек, намотанных на тороидальный сердечник.
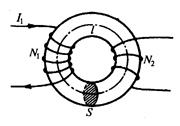
Первая катушка с числом витков
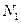
и током
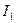
создает поле
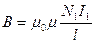
. Магнитный виток второй катушки
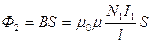
где l— длина сердечника по средней линии.
Тогда полный магнитный поток (потокосцепление) сквозь вторичную обмотку, содержащую N2 витков:
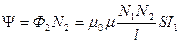
. Поскольку поток Ψ создается током
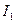
, то
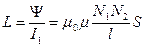
Данное устройство является примером трансформатора.
35. Трансформаторы.
Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении взаимной индукции. Переменный ток
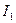
, создает в первичной обмотке переменное магнитное поле. Это вызывает во вторичной обмотке появление ЭДС взаимной индукции. При этом:
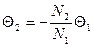
где
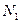
и
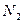
— число витков в первичной и вторичной обмотках, соответственно.
Отношение
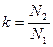
, показывающее, во сколько раз ЭДС во вторичной обмотке трансформатора больше <или меньше), чем в первичной, называется коэффициентом трансформации.
Если k>1, то трансформатор — повышающий, если к
Тогда работа по созданию магнитного потока Ф будет равна
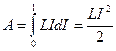
Энергия магнитного поля, связанного с контуром.
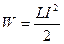
На примере однородного магнитного поля внутри длинного соленоида выразим энергию магнитного поля через величины, характеризующие это поле в окружающем пространстве.
Индуктивность соленоида:
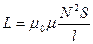
Отсюда:
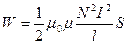
.
Магнитная индукция поля соленоида:
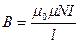
Отсюда:
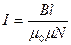
.
По определению вектора напряженности магнитного поля
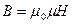
.
Используя эти соотношения
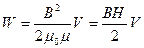
где Sl=V — объем соленоида.
Магнитное поле длинного соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и распределена в нем с объёмной плотностью
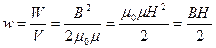
Эти соотношения носят общий характер и справедливы и для неоднородных полей, но только для сред, для которых связь между
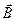
и
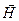
линейная (т.е. для пара- и диамагнетиков).
Выражение для объемной плотности энергии магнитного поля аналогично соответствующему выражению для объемной плотности энергии электростатического поля:
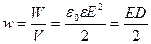
, с той разницей, что электрические величины заменены в нем магнитными.